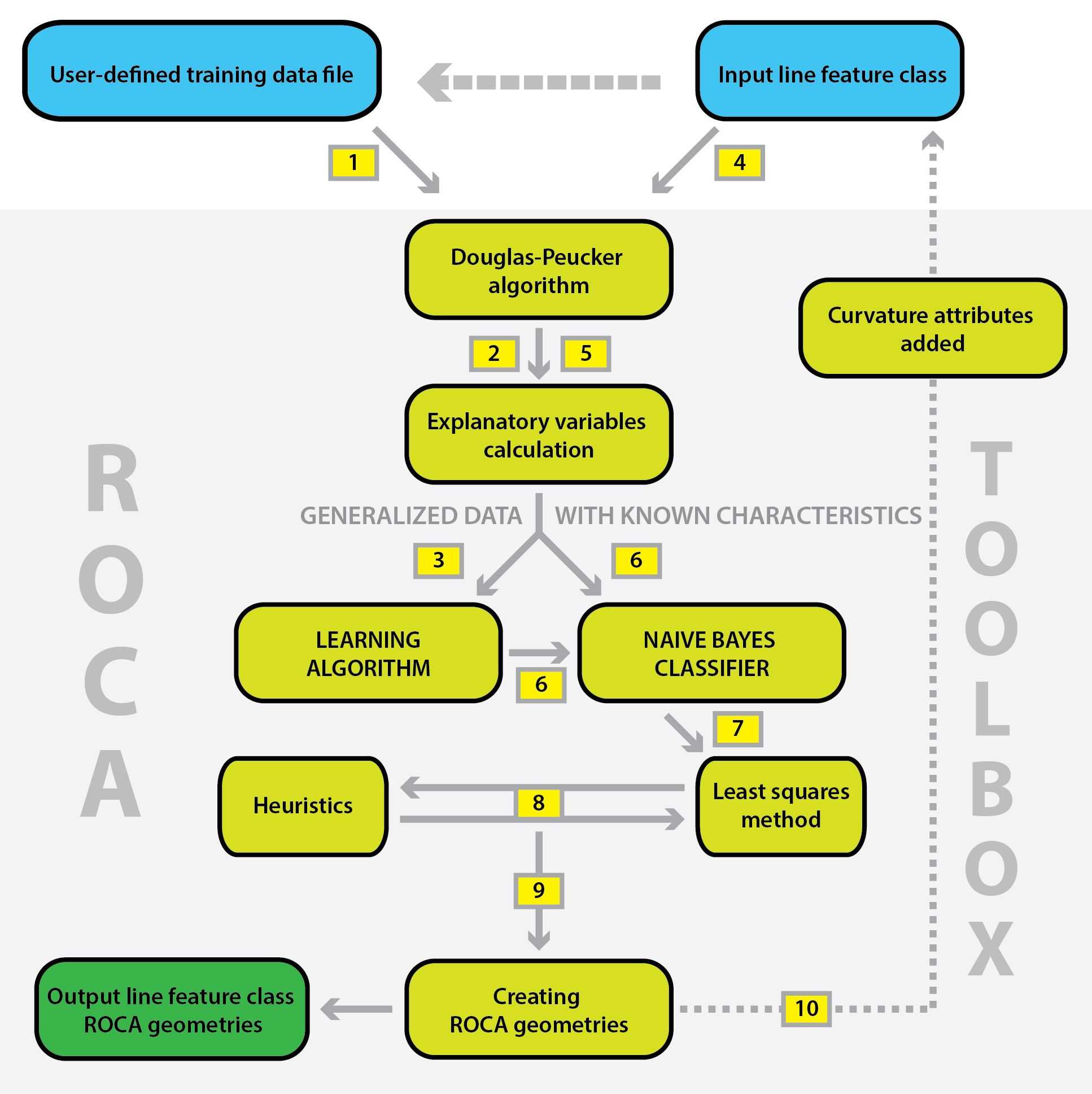
Either a user-defined training data set or a default training data set is selected (step 1). The default training data set consists of several secondary roads from the Czech road network. The training data set is generalized (step 2) and six explanatory variables (attributes) are computed for each vertex:

• radius of an osculating circle,
• radius of a circumscribed circle,
• angle between three consecutive vertices,
• cumulative angle at three vertices,
• cumulative angle at five vertices.

See Andrášik and Bíl (2016) for details. Subsequently, a naïve Bayes classifier is constructed from the training data set (step 3). The kernel density estimation is applied to calculate univariate probability densities in “tangent” and “horizontal circle” groups.

Then a user input the entire data set (step 4). Generalization is processed and explanatory variables are computed for the entire data (step 5). Then, the naïve Bayes classifier is used for identification of horizontal curves and tangents (step 6). The Least squares method (step 7) and heuristics (step 8) are applied to estimate horizontal curve radii and to identify composite horizontal curves. Finally, the output file containing individual road alignment geometry is created (step 9). Every record (road segment has the following attributes:

• ID of a line,
• type of the geometry (0 = tangent, 1 = horizontal curve),
• radius of a horizontal curve,
• coordinates of the center of a circle determining the respective horizontal curve,
• azimuth of a tangent,
• length of a segment.

Furthermore, three new fields with curvature attributes are added to the original line data file (step 10):

• detour ratio (sinuosity of a road section) as a ratio of actual (network route, polyline length) and the shortest (Euclidean) distance between endpoints of a road section,
• number of turns along a road section,
• average cumulative angle turned per kilometer of a road section.

Our approach for road geometry identification was published at first in the Journal of Geographical Systems:

Andrášik, R.; Bíl, M., 2016. Efficient Road Geometry Identification from Digital Vector Data. Journal of Geographical Systems 18(3), 249–264.

Example of the segmented Czech road network by ROCA analysis can be viewed at web-map application:

roca.cdvgis.cz/czechia